Problem komiwojażera w logistyce – obliczyć niemożliwe

Nie od dziś wiadomo, że dzięki rozwojowi informatyki, firmy uzyskują coraz lepsze wyniki w sprzedaży, nie wspominając o tym, że mogą w ogóle funkcjonować dzięki rozwiązaniom programowym. Idąc dalej, ludzie mogą załatwić coraz więcej spraw czy pracować poprzez internet. Nie każdy jednak wie, że nawet informatyka ma swoje granice i nie udzieli dokładnej odpowiedzi na wszystko, włącznie z chatGPT :).

Od lat w obrębie informatyki istnieją zagadnienia, problemy, dla których nie zostały zaproponowane efektywne i podstawne rozwiązania. Jednym z nich jest właśnie zagadnienie optymalizacyjne zwane problemem komiwojażera, które jest ściśle utożsamiane z branżą TSL. Czytaj dalej, aby dowiedzieć się, na czym polega. A może to Ty okażesz się tym szczęśliwcem, który rozwiąże ten problem?

Skąd się wziął ten “Travelling salesman problem”?

Trudno jest jednoznacznie wskazać osobę, która jako pierwsza ogłosiła trud wskazania instrukcji postępowania dla rozwiązania problemu komiwojażera (TSP). Pierwsze wzmianki o nim sięgają lat 30. XIX wieku, a pierwsze próby rozwiązania powzięto ok. 100 lat później, gdy starano się wyznaczyć optymalną trasę dla autobusu szkolnego. Analizowanie zagadnienia w oparciu o skomplikowane prawa i wyrażenia matematyczne pozostawimy naukowcom. My skupimy się na jego istocie, przedstawiając go w łatwo przyswajalny sposób.

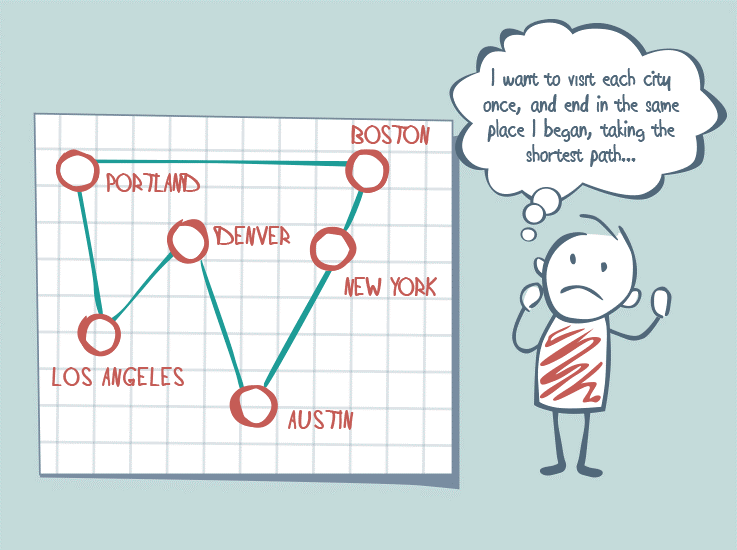
Na czym polega problem komiwojażera?

Załóżmy, że jest kurier, który zaczyna i kończy pracę w Warszawie. Pewnego dnia musi on dostarczyć paczki pod adresy w Krakowie, Wrocławiu, Białymstoku, Szczecinie, Poznaniu i Gdańsku. Problem komiwojażera polega na znalezieniu najkrótszej trasy, która pozwoli kurierowi odwiedzić te wszystkie miasta. Nie musi on dotyczyć tylko długości trasy, bowiem może również skupiać się na znalezieniu najtańszej lub najszybszej drogi. W naszym przykładzie ilość możliwych tras wynosi 5040.

Jak firmy radzą sobie z problemem TSP?

Jeśli szukamy najkrótszej trasy dla kilku miast, to znalezienie optymalnego rozwiązania może zająć sekundy lub parę minut na zwykłym komputerze. Gdy natomiast mówimy o np. 52 miastach, wówczas stosuje się różne algorytmy, równoległe i rozproszone obliczenia, które pozwalają na znalezienie – wystarczających dla logistyki – przybliżonych rozwiązań, gdyż sprawdzenie wszystkich możliwych tras jest praktycznie niemożliwe. Pewnie nie zdziwi Cię, że ma w tym swój udział sztuczna inteligencja (AI).

Zastosowania problemu komiwojażera

Problem komiwojażera ma wiele praktycznych zastosowań. Głównym i tym, dla którego piszemy ten artykuł, jest optymalizacja tras dla floty samochodowej, statków, czy samolotów, minimalizując koszty i czas dostawy. Kolejnym jest planowanie tras dla robotów w magazynach czy centrach logistycznych. TSP jest również stosowany przy projektowaniu sieci telekomunikacyjnych, aby zapewnić optymalną jakość sygnału i zminimalizować koszty.

My pomożemy Ci zoptymalizować załadunek

Może i nie jesteśmy w stanie rozwiązać problemu komiwojażera i wskazać optymalnej trasy dla dowolnej liczby miast, ale dysponujemy programem do planowania załadunku EasyCargo. Poza wyznaczeniem zarówno planu optymalnego rozmieszczenia towarów (możesz grupować je wedle miejsc rozładunku) oraz nacisku na osie przestrzeni ładunkowej, pozwala generować raporty w formacie Excel lub PDF, a nawet link publiczny do wspólnej pracy ze współpracownikami nad załadunkami.

Ponadto EasyCargo możesz zintegrować z Twoim firmowym oprogramowaniem bądź innymi programami np. telemetrycznym FleetUp za pomocą naszego API. Z jego szczegółami zapoznasz się pod tym linkiem.

Źródło: https://developer-blogs.nvidia.com/wp-content/uploads/2023/01/cuopt-featured.jpg

Właściwie można już przyznać, że dla branży TSL problem komiwojażera przestaje być powoli zmartwieniem za sprawą rozwoju, głównie sztucznej inteligencji i Big Data. Wszelkiego rodzaju oprogramowania do optymalizacji tras dostaw proponują tę, która nie odbiega znacząco od najkorzystniejszej trasy i w czasie rzeczywistym dostosowują ją w zależności od warunków na drogach.

Trzymamy kciuki, aby udało Ci się zaproponować algorytm, który dla dowolnej liczby miast wyznacza optymalną trasę w czasie co najwyżej wielomianowym!

Autor: Bartosz Ziółkowski